الحل
رياضيات ( 2 )
47 ) اكتشف الخطأ : اوجد كل من عادل وسعيد في شكل الطائرة الورقية ABCD المجاور ، هل اجابة اي منهما صحيحة ؟ وضح اجابتك.
عادل سعيد
اجابة عادل هي الصحيحة
48) تحد ، اذا كان الضلعان المتوازيان في شبه منحرف محتويين في المستقيمين y = x + 4 , y = x-8 فما معادلة المستقيم الذي يحتوى القطعة المتوسطة لشبه المنحرف ؟
القطعة المتوسطة = مجموع طول القاعدتين
y = x - 2
49) تبرير : هل العبارة ( المربع هو ايضا طائرة ورقية ) صحيحة احيانا ام دائما ام غير صحيحة ابدا ؟
غير صحيحة ابدا حيث ان اضلاع المربع الاربعة متطابقة تماما بينما لا يوجد ضلعان متقابلان في شكل الطائرة الورقية متطابقان
50) مسألة مفتوحة ، ارسم ............
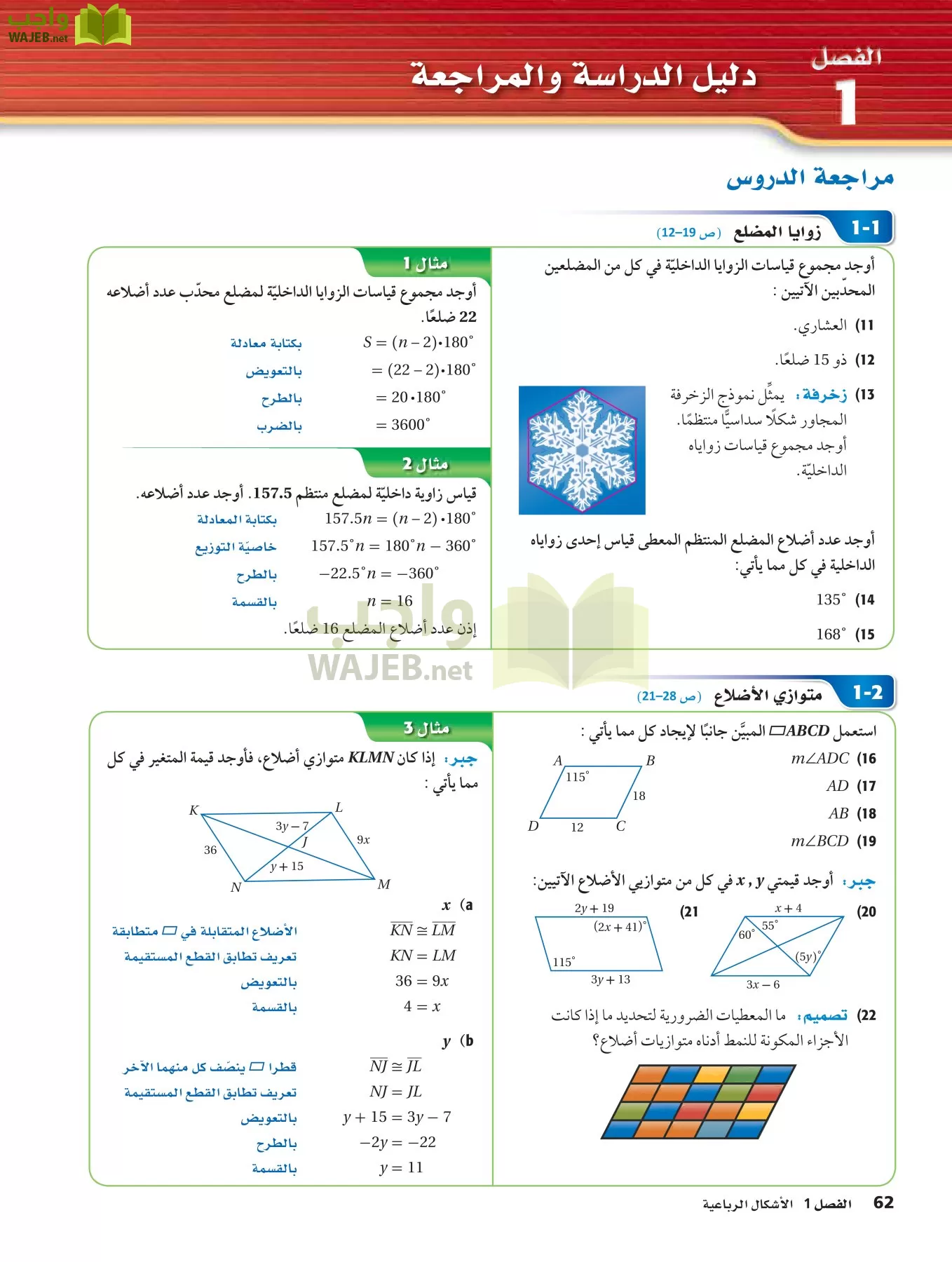
51) اكتب : قارن بين خصائص كل من شبه المنحرف وشبه المنحرف المتطابق الساقين وشكل الطائرة الورقية.
شبه المنحرف : هو شكل رباعي فيه ضلعان فيه فقط متوازيان يسميان قاعدتي شبه المنحرف ويسمى الضلعان غير المتوازيان ساقي شبه المنحرف
شبه المنحرف المتطابق الساقين : هو شكل رباعي فيه ضلعان فيه فقط متوازيان ومتطابقان وزوايا القاعدة متطابقة
الطائرة الورقية : هو شكل رباعي يتكون من زوجين متمايزين من الاضلاع المتجاورة المتطابقة وعلى عكس متوازي الاضلاع كل ضلعين متقابلين ليسا متطابقين او متوازيين
52) اجابة شبكية : اذا كان ABCD شكل طائرة ورقية فما قياس ؟
53 ) ما الشكل الذي يمكن ان يكون مثالا مضادا للتخمين الآتي ؟
اذا كان قطرا شكل رباعي متطابقين فانه مستطيل
F المربع
G المعين
H متوازي الاضلاع
J شبه المنحرف المتطابق الساقين
جبر ، استعن بالمعين DFGH فيما يأتي :
54) اذا كان فاوجد
اذن الزاويتين الاخرتين في = 180 - 118 = 62
55 ) اذا كان DM = 4x - 3 , MG = x + 6 فاوجد DG
x+6=4x-3
x = 3
DG = MG + MD
DG = x+6+4x - 3
DG = 18
56) اذا كان FM = 12 , HD = 15 فاوجد MG
HD = HG = 15
MG = 9
اوجد ميل القطعة المستقيمة المعطاة احداثيات طرفيها في كل مما يأتي :
58)
الميل
59 )
الميل
60)
الميل
الميل غير معروف