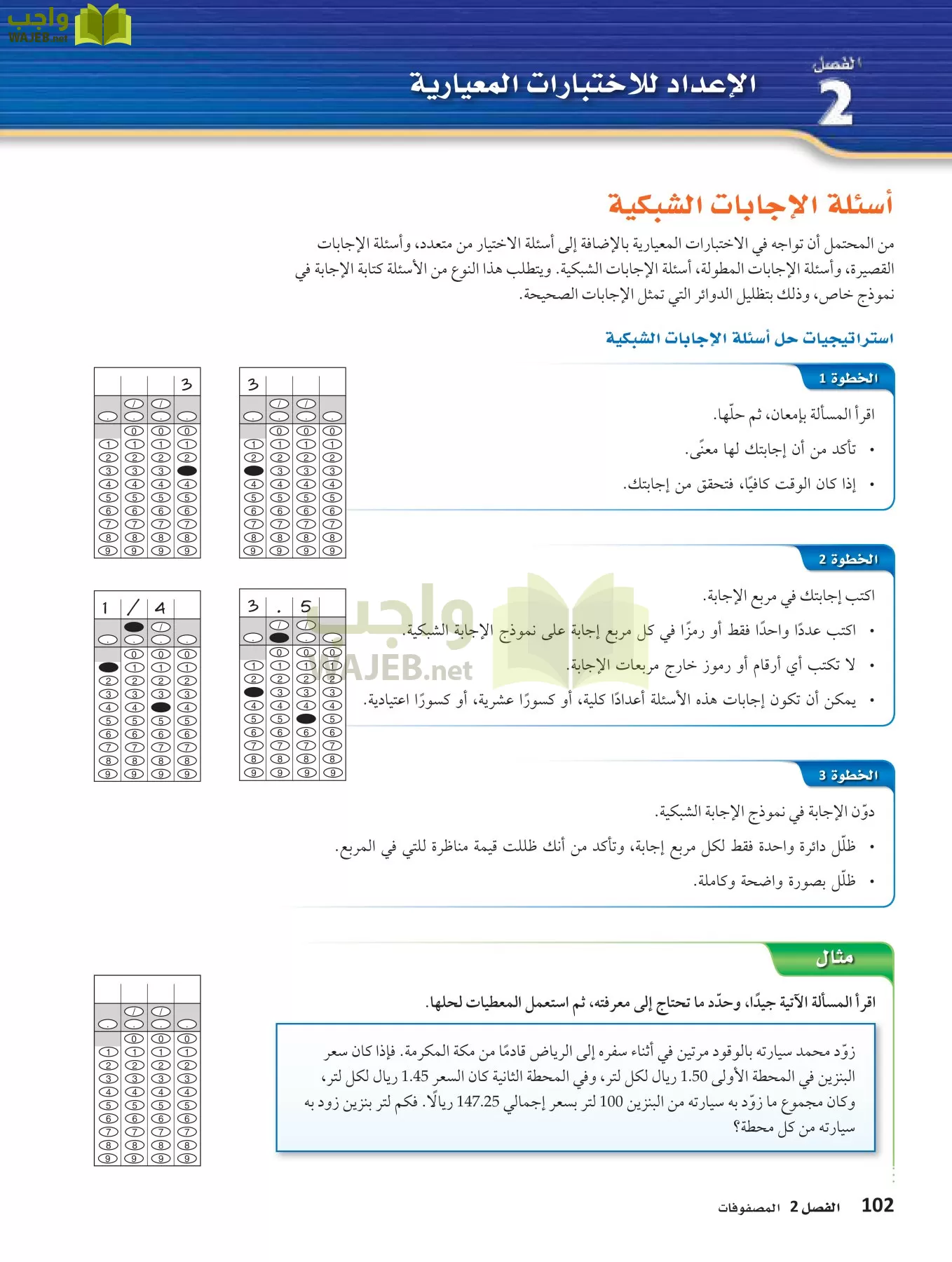
الحل
رياضيات (3) الصف الثانى الثانوى
المحددات وقاعدة كرامر
اوجد قيمة كل محددة فيما يأتى :
16)
17)
استعمل قاعدة كرامر لحل كل نظام فيما يأتى :
18)
19)
80=(4)(4)(5)
28=(7)(2)(2)
0=(3)(3)(0)
0=(0)(4)(7)
30=(5)(2)(3)
24=(2)(3)(4)
108=80+28+0
54=0+30+24
54=108-54
20) حرف يدوية :
العقد 20 ريالاً والسوار 15 ريالاً
النظير الضربى للمصفوفة وانظمة المعادلات الخطية
أوجد النظير الضربى لكل مصفوفة فيما يأتى ، ان وجد :
21)
22)
23)
لا يوجد نظير ضربى
حل المعادلات المصفوفية فى كل مما يأتى:
24)
25)