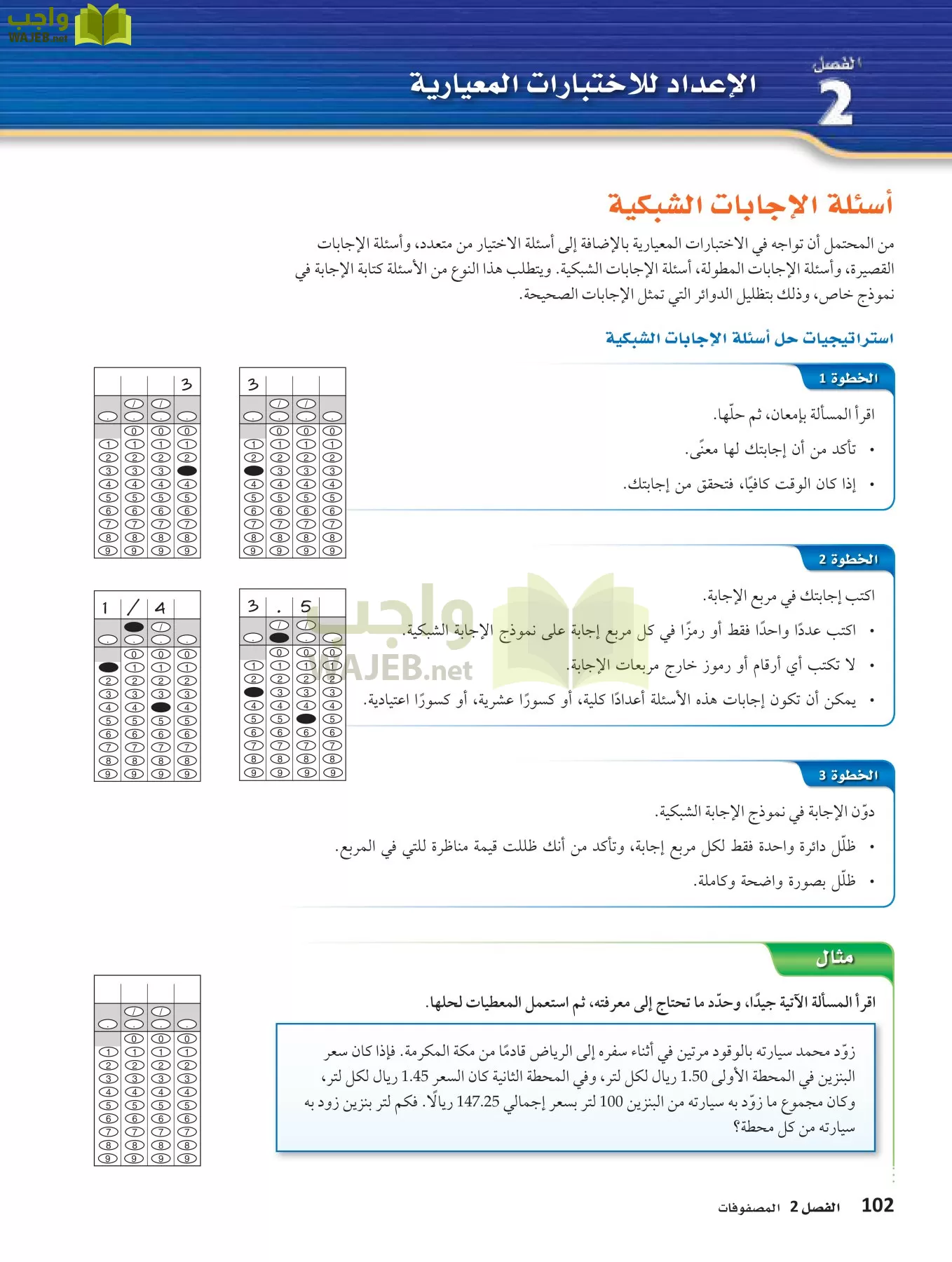
الحل
رياضيات (3) الصف الثانى الثانوى
تأكد
حدد اذا كانت كل من المصفوفتين تمثل نظير ضربييا للاخرى فيما يأتى :
1)
الاجابة لا
2)
الاجابة نعم
3)
4)
5) نقود:
نفرض أن x عدد النصف ريال y عدد الربع ريال
مع احمد 16 ربعاً و9 انصاف
استمل معادلة مصفوفية لحل كل نظام فيما يأتى :
6)
7)
8)
حدد اذا كانت كل من المصفوفتين تمثل نظير ضربياً للاخرى فيما يأتى :
9)
لا تمثل نظير ضربيباً
10)
لا تمثل نظير ضربياً
11)
لا تثمل نظير ضربياً
أوجد النظير الضربى لكل مصفوفة فيما يأتى ان وجد:
12)
13)
14)
15)
16)مشتريات :
17)سكان :
استعمل معادلة مصفوفية لحل كل نظام ان امكن فيما يأتى
18)
ليس لها حل
19)
20)
21)
22)
ليس لها حل
23)
24)
25)
26)