الفصل الاول/تحليل الدوال الفصل الثاني/العلاقات والدوال الأسية واللوغاريتمية الفصل الثالث/المتطابقات والمعادلات المثلثية الفصل الرابع/القطوع المخروطية
Search السابق 216 التالي Search Search Search
Search Search
رياضيات 5 مقررات page-16
رياضيات 5 مقررات page-17
رياضيات 5 مقررات page-18
رياضيات 5 مقررات page-19
رياضيات 5 مقررات page-20
رياضيات 5 مقررات page-21
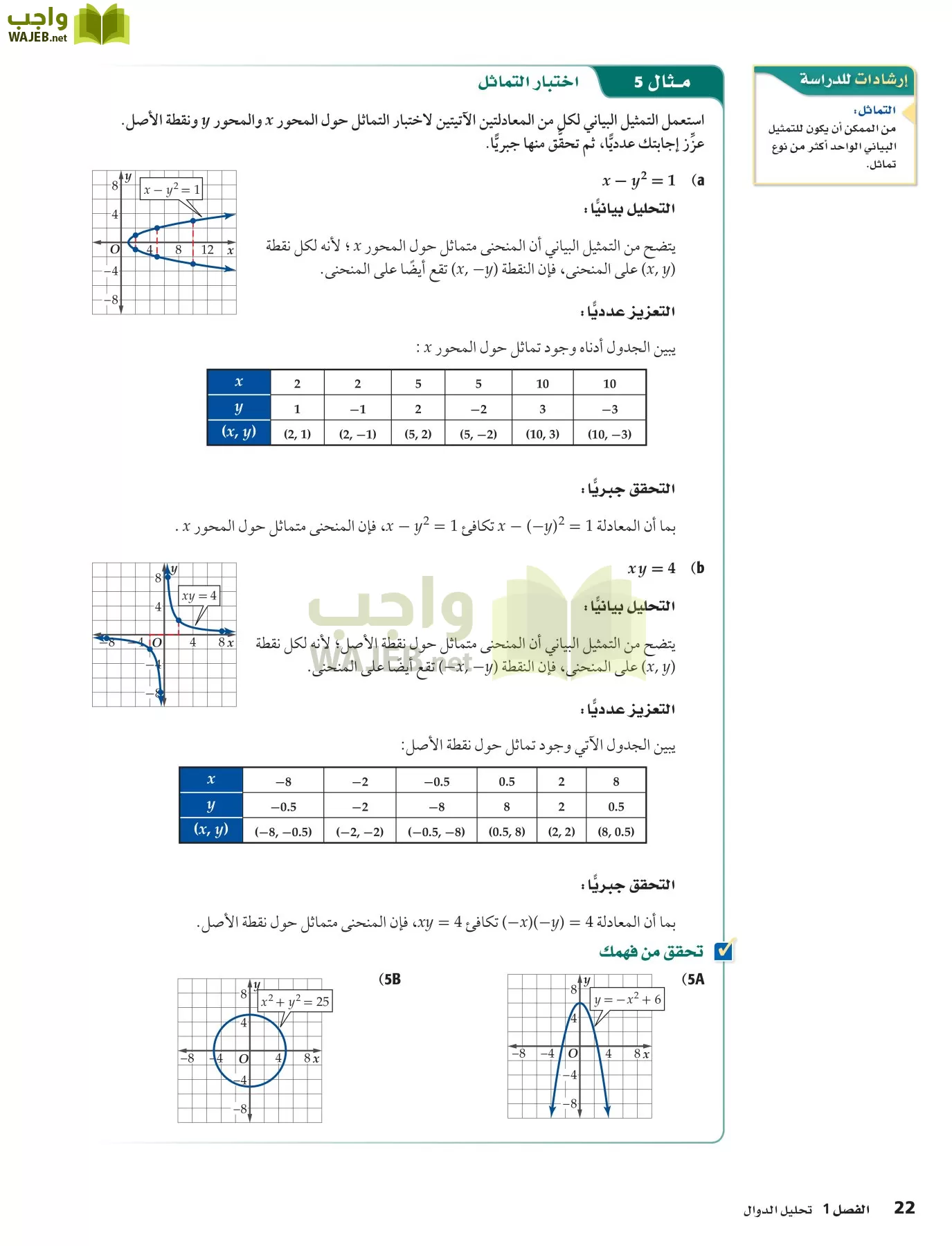
رياضيات 5 مقررات page-22
رياضيات 5 مقررات page-23
رياضيات 5 مقررات page-24
رياضيات 5 مقررات page-25
رياضيات 5 مقررات page-26

حل رياضيات 5 مقررات صفحة 16

الحل

رياضيات 5 

اوجد   f\left ( -5 \right )   و  f\left (12 \right )   لكل من الدالتين الاتيتين :

(33)

f(x)=-4x+3

f(-5)=-4*(-5)+3=23

f(x)=3x^{3}+1

f(12)=3(12)^{3}+1=433

(34)

f(x)=\sqrt{x+6}

f(-5)=\sqrt{(-5)+6}=1

f(x)=\frac{2}{x}+8

f(12)=\frac{2}{12}+8=8\frac{1}{6}

(35) عمل :

t(x)=2.1x

t(7000)=2.1*7000=14700

t(x)=5000+2.4x

t(10000)=5000+2.4*10000=29000

t(x)=8000+3x

t(50000)=8000+3*50000=158000

(36) داله لان الخط الرأسي لا يقطع المنحنى فى اكثر من  مرة

(37)  ليست داله لان الخط الرأسي يقطع التمثيل البيانى

(38)  رياضه :

(a)  

D(t)\left \{ 4t.0\leq 1\leq 0.6\right.

D(t)\left \{ 20t.0< 1\leq 6.2\right.

D(t)\left \{ 6t.6.2< 1\leq 10.7\right.

(b) مجال الداله :   \left [ 0.10.7 \right ]

(39) هندسه :

(a) r=\frac{c}{2\eta }

A=\eta *\frac{C^{2}}{4\eta ^{2}}=\frac{C^{2}}{4\eta }

(b)  A(4)=\frac{4^{2}}{4\eta }=1.27

A(0.5)=\frac{(0.5)^{2}}{4\eta }=0.2

(c) كلما زاد المحيط زادت المساحه 

(40)  حسابات   :  \upsilon (t)=1800-30t

مجال الداله هو : D=\left \{ t\left | 0\leq t\leq 60.t\varepsilon N \right | \right \}

اوجد \frac{f(a+h)+f(a)}{h} وf(a),f(a+h) حيث h\neq 0 لكل مما يأتى :

(41) f(x)=-5

f(a)=-5

f(a+h)=-5

\frac{f(a+h)-f(a)}{h}=\frac{-5-(-5)}{h}=0

(42)  f(x)=\sqrt{x}

f(a)=\sqrt{a}

f(a+h)=\sqrt{a+h}

\frac{f(a+h)-f(a)}{h}=\frac{\sqrt{a+h}-\sqrt{a}}{h}

(43)  f(x)=\frac{1}{x+4}

=\frac{a+4-a-h-4}{(a+h+4)(a+4)}*\frac{1}{h}

\frac{f(a+h)-f(a)}{h}=\frac{\frac{1}{a+h+4}-\frac{1}{a+4}}{h}

(44)  f(x)=x^{2}-6x+8

\frac{f(a+h)-f(a)}{h}=\frac{h(h+2a+6)}{h}=h+2a-6

(45)  f(x)=-14x+6

\frac{f(a+h)-f(a)}{h}=\frac{-14a-14h+6+14a-6}{h}=-14

(46)  f(x)=x^{2}+9

\frac{f(a+h)-f(a)}{h}=\frac{h(h^{2}3ah+3a^{2})}{h}=h^{2}+3ah+3a^{2}

(47)   f(x)=5x^{2}

\frac{f(a+h)-f(a)}{h}=\frac{h(5h+10a)}{h}=5h+10a

(48)  f(x)=x^{3}

\frac{f(a+h)-f(a)}{h}=\frac{h(h^{2}+3ah+3a^{2})}{h}=h^{2}+3ah+3a^{2}

(49)

(a)                 A(L)=\frac{L^{2}}{1.8}

            مجال الداله هو :  \left [ 5,11,5 \right ]

(b)               A(h)=2.1h^{2}

            مجال الجداله هو \left [ 2.4,5,5 \right ]

(c)           A=52.9 in^{2}

حدد ما اذا كانت  y  داله فى x أم لا 

(50)  x=\left | y \right |

ليست داله لان لكل قيمه  x  فى المجال توجد قيمتان y

(51)   x=x^{2}

داله لان لكل قيمه  x   فى المجال يوجد قيمه واحدة y

أظهر المزيد من الحل إخفاء جزء من الحل
الفصل الاول/تحليل الدوال

الفصل الاول/تحليل الدوال
الفصل الثاني/العلاقات والدوال الأسية واللوغاريتمية

الفصل الثاني/العلاقات والدوال الأسية واللوغاريتمية
الفصل الثالث/المتطابقات والمعادلات المثلثية

الفصل الثالث/المتطابقات والمعادلات المثلثية
الفصل الرابع/القطوع المخروطية

الفصل الرابع/القطوع المخروطية
Search Search

مواد اخرى لعلوم طبيعية من المرحلة الثانوية مقررات