السابق 216 التالي

حل رياضيات 5 مقررات صفحة 35

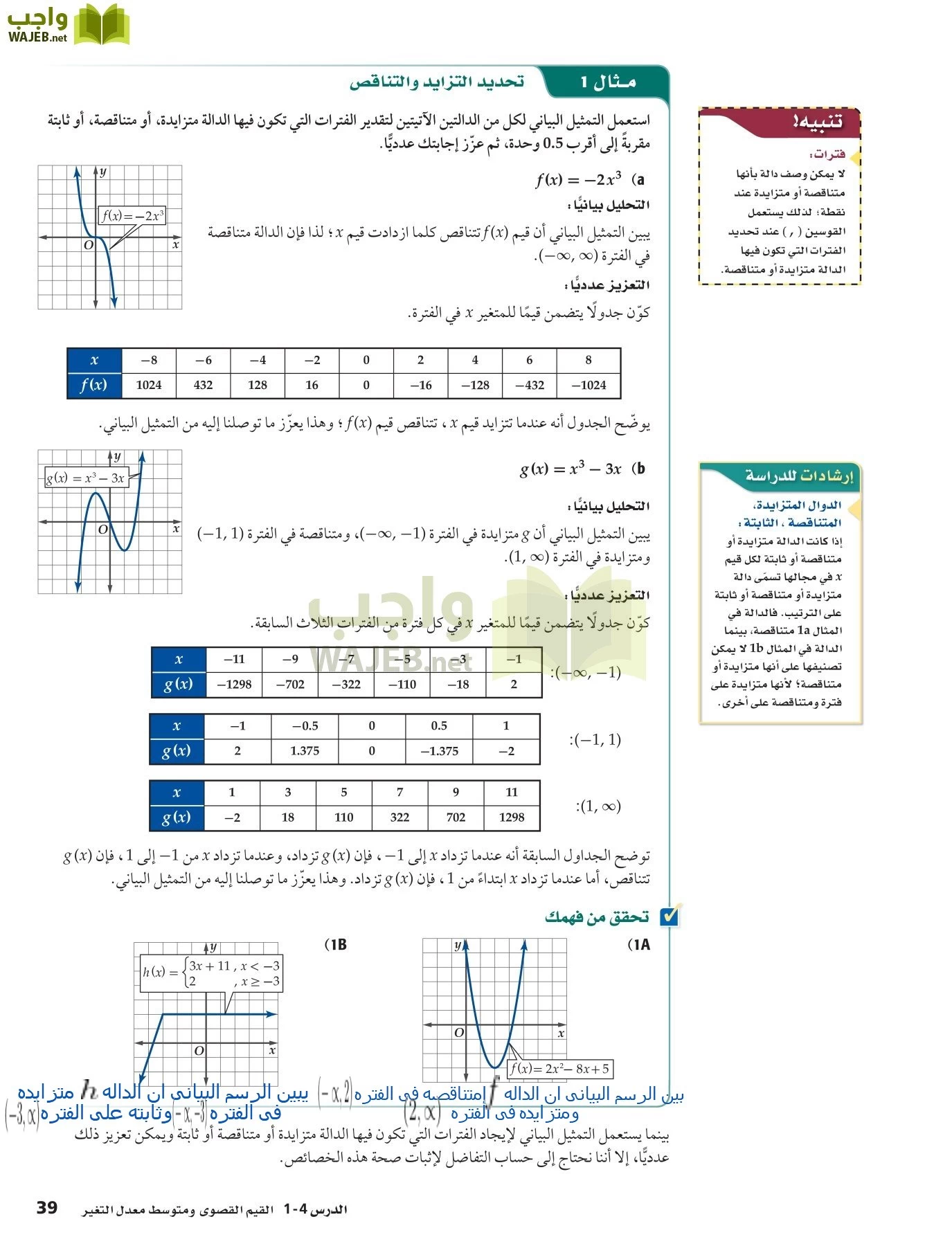
الحل

رياضيات 5

تدرب وحل المسائل:

حدد مااذا كانت كل دالة ما يأتى متصلة عند قيمة x المعطاة وبرر اجابتك باستعمال اختبار الاتصال اذا كانت الدالة غير متصلة فحدد نوع عدم الاتصال لا نهائى قفزى قابل للزالة .

1) الدالة معرفه عند x=-5 وتؤول قيم الدالة الى 3,61 عندما تقترب x من 8 من الجهتين $f(8)=3.61$ والداله متصلة عند 8

2) الدالة معرفه عند x=8 وتؤول قيم الدالة الى 3,61 عندما تقترب x من 8 من الجهتين $f(8)=3.61$ والداله متصلة عند 8

3)الدالة غير متصله اتصال قابل للازاله عند x=-b الداله معرفه عند x=b تقترب قيم الداله الى 0 عندما تقترب x من 0 من الجهتين $h(6)=0$ الداله متصله عند

4) الدالة غير متصلة اتصال لا نهائى عند x=1

5) الدالة غير متصله اتصال قابل للازاله عند x=4 والدالة غير متصله اتصال لا نهائى عند x=1 وقيم الدالة تقترب من 1/3 عند $x\rightarrow 4$ من الجهتين

6)الدالة غير متصله اتصال قابل للازاله عند x=0 الداله معرفه عند x=6 تقترب قيم الداله الى 0 عندما تقترب x من $x\rightarrow 6$ من الجهتين $h(6)=0$ الداله متصله عند x=6

7) الدالة غير متصلة اتصال قفزى عند x=-6 حيث $f(x)=6$ تقترب من 8 عندما تقترب $x\rightarrow- 6$ من جهه اليمين

فيزياء :

(8)

a: الداله متصله .. (1)التبرير $f(0.4)=18.5$

(2):يتبين من الجدول ان $limf(\bowtie )=18.5$

(3) $f(\bowtie )$ متصله عند $(\bowtie )=0.4$ لان $limf(\bowtie )=18.5$

(b) يتضح من الرسم البيانى ان الدالة غير متصلة ( لا نهائى ) عند $(\bowtie )=0$ لان الدالة تقترب من قيمتين مختلفتين على يمين ويسار العدد 0

اعد تعرف الداله لتصبح متصلة عند x=-3

1- $f(-3)=\frac{0}{0}$

2: ابحث فى قيم الدالة عندما تقترب x من -3

-2.9	-2.99	-2.999	-3	-3.001	-3.01	-3.1	x
-5.9	-5.99	-5.999		-6.001	-6.01	-6.1	$f(x)$

قيم $f(x)$ تقترب من -6 عندما تقترب x من -3 من الجهتين اى ان $limf(x=-6$

$f(x)$ غير متصله عند x=-6 لان $f(-3)$ غير موجودة وبما ان $limf(x)$ موجوده فان عدم الاتصال قابل للزالة عند x=-3

3- $f(x)=\left \{ \frac{x^{3}-9}{x+3} :x\neq -3, -6 :x= -3\right.$

(10) اعد تعرف الداله $f(-3)=\frac{x^{2}-25}{x-5}$ لتصبح متصلة عند x=5

1. $f(5)=\frac{0}{0}$

2- ابحث فيم قيك الداله عندما تقترب x من -3

5.1	5.01	5.001	5	4.999	4.99	4.9	x
10.1	10.01	10.001		9.999	9.99	9.9	$f(x)$

قيم $f(x)$ تقترب من 10 عندما تقترب x من 5 من الجهتين اى ان $limf(x)=10$

$f(x)$ غير متصله عند $x=10$ لان $f(5)$ غير موجودة وبما ان $limf(x)$ موجوده فان عدم الاتصال قابل للزالة عند $x=5$

(3) : $f(x)=\frac{x^{2}-25}{x-5}: x\neq 5 , 10 : x=5$

(11) اعد تعرف الدالة $f(x)=\frac{x^{2}-2}{x-\sqrt{2}}$ لتصبح متصله عند $x=\sqrt{2}$

1: $(\sqrt{2})=\frac{0}{0}$

2: ابحث فى القيم الداله عندما تقترب x من $\sqrt{2}$

. $\sqrt{2.1}$	$\sqrt{2.01}$	$\sqrt{2.001}$	$\sqrt{2}$	$\sqrt{1.999}$	$\sqrt{1.99}$	$\sqrt{1.9}$	$x$
2.863	2.832	2.82878		2.82807	2.825	2.792	$f(x)$

يظهر فى الجدول اعلاء ان قيم $f(x)$ تقترب من 2.8285 عمدما تقترب من $\sqrt{2}$ من الجهتين اى ان $limf(x)=2.8285$

$f(x)$ غير متصلة عند 2.885=x لان $f(\sqrt{2})$ غير موجودة وبما ان $limf(x)$ موجوده فان عدم الاتصال قابل للزاله عند $x=\sqrt{2}$

$f(x)=\left \{ \; \frac{x^{2}-2}{x-\sqrt{2}}x\neq \sqrt{2},,2.385:x=\sqrt{2} \right.$

(12) فى الفتره المعطاه :

$f(x)=x^{3}-x^{2}-3$ فى الفتره

4	3	2	1	0	-1	-2	$x$
45	15	1	-3	-3	-5	-15	$f(x)$

بما ان $f(x)$ سالبة و $f(2)$ موجبة

$\therefore$ يوجد صفر للدالة $f(x)$ فى الفتره $\left [ 1.2 \right ]$

(13) $g(x)=-x^{3}+6x+2$ فى الفترة $\left [ -4.4 \right ]$

4	3	2	1	0	-1	-2	-3	-4	$x$
-38	-7	6	7	2	-3	-2	11	42	$g(x)$

بما ان $g(-3)$ موجبه و $g(-2)$ سالبة $\therefore$ يوجد صفر للدالة $g(x)$ فى الفترة $\left [ -3.-2 \right ]$

وكذلك يوجد صفر للدالة $g(x)$ لإى الفتره $\left [ -1.0 \right ],,\left [ 2.3 \right ]$

(14) $f(x)=2x^{4}-3x^{3}+x^{2}-3$ فى الفترة $\left [ -3.3 \right ]$

3	2	1	0	-1	-2	-3	$x$
87	9	-3	-3	3	57	249	$f(x)$

بما ان $f(-1)$ موجبة و $f(0)$ سالبة $\therefore$ يوجد صفر للدالة

$f(x)$ فى الفترة $\left [ -1.0 \right ]$ وكذلك يوجد صفر للدالة $f(x)$ فى الفترة $\left [ 0.1 \right ]$

(15) $h(x)=\frac{x^{2}+4}{x-5}$ فى الفترة $\left [ -2.4 \right ]$

4	3	2	1	0	-1	-2	$x$
-20	-6.5	-2.67	-1.25	-0.8	-0.83	-1.14	$h(x)$

من بيانات الجدول ومن الرسم البيانى يتضح انه لا يوجد اصفار للدالة $h(x)$

(16) $g(x)=\sqrt{x^{2}+1}-5$ فى الفترة $\left [ 0.5 \right ]$

5	4	3	2	1	0	$x$
6.22	3.06	0.29	-2	-3.59	-4	$g(x)$

بما ان $g(2)$ موجبة و $g(3)$ سالبة $\therefore$ يوجد صفر للدالة

$g(x)$ فى الفترة $\left [ 2.3 \right ]$

استعمل التمثيل البيانى لكل من الدوال الاتية لوصف سلوك طرفى تمثيلها البيانى ثم عزز اجابتك عددياً

(17) واضح من الرسم ان $f(x)\rightarrow \bowtie$ عندما $(x)\rightarrow \bowtie$ وكذلك $f(x)\rightarrow \bowtie$ عندما $f(x)\rightarrow -\bowtie$

10000	1000	100	0	-100	-1000	-10000	$x$
$4.10^{16}$	$4.10^{12}$	$4.10^{8}$	$0$	$4.10^{8}$	$4.10^{12}$	$4.10^{16}$	$f(x)$

(18) واضح من الرسم ان $f(x)\rightarrow \bowtie$ عندما $x\rightarrow -\bowtie$ و $f(x)\rightarrow -\bowtie$ عندما $x\rightarrow \bowtie$

10000	1000	0	-1000	-10000	$x$
- $5.10^{12}$	- $5.10^{9}$	-1	$5.10^{9}$	$5.10^{12}$	$f(x)$

(19) واضح من الرسم ان $f(x)\rightarrow \bowtie$ عندما $x\rightarrow \bowtie$ وكذلك $f(x)\rightarrow -\bowtie$ عندما $x\rightarrow -\bowtie$

10000	1000	0	-1000	-10000	$x$
10005	1005	-0.333	-995	-9995	$f(x)$

(20) واضح من الرسم ان $f(x)\rightarrow -4$ عندما $x\rightarrow \bowtie$ وكذلك $f(x)\rightarrow -4$ عندما $x\rightarrow -\bowtie$

10000	1000	0	-1000	-10000	$x$
-4.001	-4.019	-0.833	-3.981	-3.998	$f(x)$

(21) واضح من الرسم ان $f(x)\rightarrow \bowtie$ عندما $(x)\rightarrow \bowtie$ وكذلك $f(x)\rightarrow- \bowtie$ عندما $x\rightarrow -\bowtie$

(22) ,واضح من الرسم ان $f(x)\rightarrow -2$ عندما $x\rightarrow \bowtie$ وكذلك $f(x)\rightarrow -2$ عندما $x\rightarrow -\bowtie$

1000	10	0	-10	-1000	$x$
-1.999999	-1.98	-5	-1.99	-1.999999	$f(x)$

(23) كيمياء :

يبين سلوك طرفى التمثيل البيانى انه اذا زاد تركيز العامل المساعد فأن معدل التفاعل الكيميائى يقترب من 0.5

أظهر المزيد من الحل إخفاء جزء من الحل

حل رياضيات 5 مقررات صفحة 35

الحل

الفصل الاول/تحليل الدوال

الفصل الثاني/العلاقات والدوال الأسية واللوغاريتمية

الفصل الثالث/المتطابقات والمعادلات المثلثية

الفصل الرابع/القطوع المخروطية

مواد اخرى لعلوم طبيعية من المرحلة الثانوية مقررات

انجليزي 4 مقررات

كيمياء 3 مقررات

انجليزي 3 مقررات

رياضيات 4 مقررات

رياضيات 6 مقررات

أحياء 2 مقررات

فيزياء 2 مقررات

انجليزي 5 مقررات

كيمياء 2 مقررات